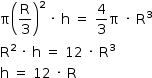Uma indústria de perfumes embala seus produtos, atualmente, em frascos esféricas de raio R, com volume dado
por 4/3π(R)³. Observou-se que haverá redução de custos se forem utilizados frascos cilíndricos com raio da base R/3 , cujo
volume será dado por π. (R/3)²h, sendo h a altura da
nova embalagem.
Para que seja mantida a mesma capacidade do frasco
esférico, a altura do frasco cilíndrico (em termos de R)
deverá ser igual a
a) 2R.
b) 4R.
c) 6R.
d) 9R.
e) 12R.
Para que a capacidade do frasco cilíndrico seja igual a capacidade do frasco esférico, devemos ter: