01. (OSEC) - A soma dos dez primeiros termos de uma P. A. de primeiro termo 1,87 e de razão 0,004 é:
a) 18,88
b) 9,5644
c) 9,5674
d) 18,9
e) 21,3
02. (UE – PONTA GROSSA) - A soma dos termos de P. A. é dada por Sn = n² – n, n = 1, 2, 3, … Então o 10° termo da P. A vale:
a) 18
b) 90
c) 8
d) 100
e) 9
03. (UNICID) - A soma dos múltiplos de 5 entre 100 e 2000, isto é, 105 + 110 + 115 + … + 1995, vale:
a) 5870
b) 12985
c) 2100 . 399
d) 2100 . 379
e) 1050 . 379
04. (ESPM Sul) - A sequência 2.x!, (x + 1)!, (x + 2)!/3 é uma progressão aritmética estritamente crescente. A razão dessa PA é igual a:
a) 3
b) 4
c) 1
d) 2
e) 5
05. (Mackenzie) - As medidas dos lados de um triângulo retângulo estão em progressão aritmética. Se a área do triângulo é 1/6, o seu perímetro é
a) 12
b) 5/6
c) 4
d) 2
e) 7/6
06. (FGV-SP) - Guilherme pretende comprar um apartamento financiado cujas prestações mensais formam uma progressão aritmética decrescente; a primeira prestação é de R$ 2 600,00 e a última, de R$ 2 020,00.
A média aritmética das prestações é um valor:
a) entre R$ 2 250,00 e R$ 2 350,00
b) entre R$ 2 350,00 e R$ 2 450,00
c) menor que R$ 2 250,00
d) maior que R$ 2 450,00
e) impossível de determinar com as informações dadas
07. (MACK-SP) - O trigésimo primeiro termo de uma progressão aritmética de primeiro termo 2 e razão 3 é:
a) 63
b) 65
c) 92
d) 95
e) 98
08. (UFGD) - Pafúncio e Marocas tiveram cinco filhos. Colocando as idades dos filhos em ordem crescente, as três primeiras estão em progressão aritmética (P.A.) e as três últimas estão em progressão geométrica (P.G.), ambas de razão 2. Sabendo que a idade do mais velho é igual à soma das idades dos demais filhos, pode-se concluir que a diferença de idade entre o mais velho e o caçula é de
a) 20 anos.
b) 21 anos.
c) 22 anos.
d) 23 anos.
e) 24 anos.
09. (UFF) - Ao se fazer um exame histórico da presença africana no desenvolvimento do pensamento matemático, os indícios e os vestígios nos remetem à matemática egípcia, sendo o papiro de Rhind um dos documentos que resgatam essa história. Nesse papiro encontramos o seguinte problema: “Divida 100 pães entre 5 homens de modo que as partes recebidas estejam em progressão aritmética e que um sétimo da soma das três partes maiores seja igual à soma das duas menores.”
Coube ao homem que recebeu a parte maior da divisão acima a quantidade de
a) 115/3 pães.
b) 55/6 pães.
c) 20 pães.
d) 65/6 pães.
e) 35 pães.
10. (UNIR) - Foi distribuída, entre três pessoas (A, B e C), uma certa quantia em dinheiro da seguinte forma: 1 real para A, 2 reais para B, 3 reais para C, 4 reais para A, 5 reais para B, 6 reais para C e assim por diante até o dinheiro acabar. Sabendo-se que o último valor recebido por C foram 300 reais, é correto afirmar que o total, em reais, recebido por A, B e C é, respectivamente:
a) 16750, 14750, 18750
b) 17500, 18500, 19500
c) 14950, 15050, 15150
d) 12850, 13850, 14850
e) 14950, 15000, 15050
11. (UNEAL) - Seja S a soma dos múltiplos de 3 compreendido entre 11 e 100. Podemos afirmar que o valor de S é igual a
a) 1.280.
b) 1.279.
c) 1.385.
d) 1.665.
e) 1.705.
12. (FEI-SP) - A razão de uma PA de 10 termos, onde o primeiro termo é 42 e o último é –12, vale:
a) -5
b) -9
c) -6
d) -7
e) 0
13. (MACK-SP) - O produto das raízes da equação x² + 2x – 3 = 0 é a razão de uma PA de primeiro termo 7. O 100º termo dessa PA é:
a) -200
b) -304
c) -290
d) -205
e) -191
14. (FGV-SP) - A soma do 4º e 8º termos de PA é 20; o 31º termo é o dobro do 16º termo. Determine a PA:
a) (-5, -2, 1, …)
b) (5, 6, 7, …)
c) (0, 2, 4, …)
d) (0, 3, 6, 9, …)
e) (1, 3, 5, …)
15. (PUC-PR) - Se em uma PA de 7 termos, de razão K, retirarmos o segundo, terceiro, quinto e sexto termos, a sucessão restante é uma PA de razão:
a) k
b) 2k
c) k/2
d) 3k
e) 5k
16. (UFRGS) - Considere as igualdades abaixo.
I) (1–2i)(1+2i) = 5 , sendo i a unidade imaginária.
II) 20 + 2-1 + 2-2 + 2-3 + ... = 2
III) 1 – 2 + 3 – 4 + 5 – 6 + ... + 99 – 100 = 50
Quais igualdades são verdadeiras?
a) Apenas I.
b) Apenas III.
c) Apenas I e II.
d) Apenas II e III.
e) I, II e III.
17. (ENEM) - Ronaldo é um garoto que adora brincar com números. Numa dessas brincadeiras, empilhou caixas numeradas de acordo com a sequência conforme mostrada no esquema a seguir.
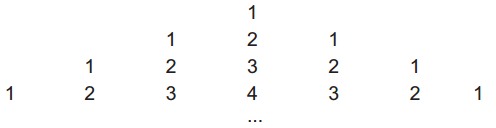
Ele percebeu que a soma dos números em cada linha tinha uma propriedade e que, por meio dessa propriedade, era possível prever a soma de qualquer linha posterior às já construídas. A partir dessa propriedade, qual será a soma da 9ª linha da sequência de caixas empilhadas por Ronaldo?
a) 9
b) 45
c) 64
d) 81
e) 285
18. (ADVISE) - Seja (a, b, c) uma progressão aritmética de razão real e de termos não nulos. Sendo assim podemos sempre afirmar que:
a) a + b = b + c
b) b = a + c
c) b² = ac
d) a – 2b + c = 0
e) 2c = a + b
19. (UDESC) - Sejam x, y, z números reais tais que a seqüência (x, 1, y, 1/4, z) forma, nesta ordem, uma progressão aritmética, então o valor da soma x + y + z é:
a) -3/8
b) 21/8
c) 15/8
d) 2
e -19/8
20. (PUC RIO) - Numa progressão aritmética de razão r e primeiro termo 3, a soma dos primeiros n termos é 3n², logo, a razão é:
a) 2
b) 3
c) 6
d) 7
e) 9
A
| A | E | D | D | A | C | C | A | C |
