01. (Cesgranrio) - A distância entre os pontos M(4, -5) e N(-1, 7) do plano x0y vale:
a) 14.
b) 13.
c) 12.
d) 9.
e) 8.
02. (FEI-SP) - Num sistema de coordenadas cartesianas são dados os pontos A(0 , 0) e P(3 , h). Assinale a alternativa cuja expressão representa a distância do ponto P ao ponto A em função de h.
a) d = √(9+h²)
b) d = h + 3
c) d = 3h
d) d = √(9 + 6h + h²)
e) d = 9 + h
03. (CFSD/PM-PA) - Os pontos (2,3), (5,3) e (2,7) são vértices de um triângulo retângulo. A área desse triângulo é:
A) 5ua
B) 6ua
C) 7ua
D) 8ua
E) 9ua
04. (PUC) - O ponto B = (3, b) é equidistante dos pontos A = (6, 0) e C = (0, 6). Logo, o ponto B é:
a) (3, 1).
b) (3, 6).
c) (3, 3).
d) (3, 2).
e) (3, 0).
05. (UFRGS) - Se um ponto P do eixo das abcissas é equidistante dos pontos A(1, 4) e B(- 6, 3), a abscissa de P vale:
a) -2
b) -1
c) 0
d) 1
e) 3
06. (Uel) - Seja AB uma diagonal do quadrado ABCD. Se A = (-2, 3) e C = (0, 5), a área de ABCD, em unidades de área, é
a) 4
b) 4√2
c) 8
d) 8√2
e) 16
07. (UFRGS) - A distância entre os pontos A (-2, y) e B (6, 7) é 10. O valor de y é:
a) -1
b) 0
c) 1 ou 13
d) -1 ou 10
e) 2 ou 12
08. (Cesgranrio) - A área do triângulo, cujo vértices são (1,2), (3,4) e (4,-1), é igual a:
a) 6.
b) 8.
c) 9.
d) 10.
e) 12.
09. (ENEM) - Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:
A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas
a) (65 ; 35)
b) (53 ; 30)
c) (45 ; 35)
d) (50 ; 20)
e) (50 ; 30)
10. (Puccamp) - Sabe-se que os pontos A = (0; 0), B = (1; 4) e C = (3; 6) são vértices consecutivos do paralelogramo ABCD. Nessas condições, o comprimento da BD é:
a) √2
b) √3
c) 2√2
d) √5
e) 5
11. (FGV) - No plano cartesiano, o triângulo de vértices A(1, -2), B(m, 4) e C(0, 6) é retângulo em A. O valor de m é igual a:
a) 47
b) 48
c) 49
d) 50
e) 51
12. (Unesp) - O triângulo PQR, no plano cartesiano, de vértices P = (0, 0), Q = (6, 0) e R = (3, 5), é
a) equilátero.
b) isósceles, mas não equilátero.
c) escaleno.
d) retângulo.
e) obtusângulo.
13. (ENEM) - Um bairro de uma cidade foi planejado em uma região plana, com ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho. No plano de coordenadas cartesianas seguinte, esse bairro localiza-se no segundo quadrante, e as distâncias nos eixos são dadas em quilômetros.
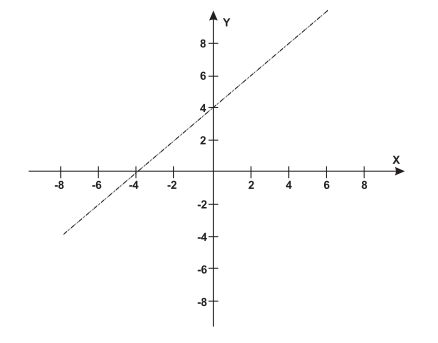A reta de equação y = x + 4 representa o planejamento do percurso da linha do metrô subterrâneo que atravessará o bairro e outras regiões da cidade. No ponto P = (–5, 5), localiza-se um hospital público. A comunidade solicitou ao comitê de planejamento que fosse prevista uma estação do metrô de modo que sua distância ao hospital, medida em linha reta, não fosse maior que 5 km.
Atendendo ao pedido da comunidade, o comitê argumentou corretamente que isso seria automaticamente satisfeito, pois já estava prevista a construção de uma estação no ponto
a) (–5, 0).
b) (–3, 1).
c) (–2, 1).
d) (0, 4).
e) (2, 6).
14. (UFF) - A palavra “perímetro” vem da combinação de dois elementos gregos: o primeiro, perí, significa “em torno de”, e o segundo, metron, significa “medida”. O perímetro do trapézio cujos vértices têm coordenadas (−1, 0), (9, 0), (8, 5) e (1, 5) é:
a) 10 + √29 + √26
b) 16 + √29 + √26
c) 22 + √26
d) 17 + 2√26
e) 17 + √29 + √26
15. (UEA) - Em um mesmo sistema de eixos cartesianos ortogonais, as representações gráficas das funções reais f(x) = x² – 2x – 3 e g(x) = – x² + 4x – 5 são parábolas. A distância entre os seus vértices é igual a:
a) 3√2
b) √26
c) √10
d) 2√3
e) 2√10
16. (PUC-RJ) - Sabendo que o ponto B = (3,b) é equidistante dos pontos A = (6,0) e C = (0,6), então b vale:
a) 1
b) 2
c) 3
d) 4
e) 5
17. (PUC-RJ) - Se os pontos A = (-1, 0), B = (1, 0) e C = (x, y) são vértices de um triângulo equilátero, então a distância entre A e C é:
a) 1
b) 2
c) 4
d) √2
e) √3
18. (UFMG) - Seja Q (-1, a) um ponto do 3º quadrante.O valor de a, para que a distância do ponto P (a, 1) ao ponto Q seja igual a 2, é:
a) - 1 - √2
b) 1 - √2
c) 1 + √2
d) -1 + √2
e) - 1
19. (ITA - SP) - Três pontos de coordenadas,respectivamente, (0, 0), (b, 2b) e (5b, 0), com b > 0, são vértices de um retângulo. As coordenadas do quarto vértice são dadas por:
a) (- b, - b)
b) (2b, - b)
c) (4b, - 2b)
d) (3b, - 2b)
e) (2b, - 2b)
20. (PUC - SP) - Dados A(4, 5), B(1, 1) e C(x, 4), o valor de x para que o triângulo ABC seja retângulo em B é:
a) 3
b) 2
c) 0
d) - 3
e) - 2
b) 8.
c) 9.
d) 10.
e) 12.
09. (ENEM) - Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:
a) (65 ; 35)
b) (53 ; 30)
c) (45 ; 35)
d) (50 ; 20)
e) (50 ; 30)
10. (Puccamp) - Sabe-se que os pontos A = (0; 0), B = (1; 4) e C = (3; 6) são vértices consecutivos do paralelogramo ABCD. Nessas condições, o comprimento da BD é:
a) √2
b) √3
c) 2√2
d) √5
e) 5
11. (FGV) - No plano cartesiano, o triângulo de vértices A(1, -2), B(m, 4) e C(0, 6) é retângulo em A. O valor de m é igual a:
a) 47
b) 48
c) 49
d) 50
e) 51
12. (Unesp) - O triângulo PQR, no plano cartesiano, de vértices P = (0, 0), Q = (6, 0) e R = (3, 5), é
a) equilátero.
b) isósceles, mas não equilátero.
c) escaleno.
d) retângulo.
e) obtusângulo.
13. (ENEM) - Um bairro de uma cidade foi planejado em uma região plana, com ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho. No plano de coordenadas cartesianas seguinte, esse bairro localiza-se no segundo quadrante, e as distâncias nos eixos são dadas em quilômetros.
Atendendo ao pedido da comunidade, o comitê argumentou corretamente que isso seria automaticamente satisfeito, pois já estava prevista a construção de uma estação no ponto
a) (–5, 0).
b) (–3, 1).
c) (–2, 1).
d) (0, 4).
e) (2, 6).
14. (UFF) - A palavra “perímetro” vem da combinação de dois elementos gregos: o primeiro, perí, significa “em torno de”, e o segundo, metron, significa “medida”. O perímetro do trapézio cujos vértices têm coordenadas (−1, 0), (9, 0), (8, 5) e (1, 5) é:
a) 10 + √29 + √26
b) 16 + √29 + √26
c) 22 + √26
d) 17 + 2√26
e) 17 + √29 + √26
15. (UEA) - Em um mesmo sistema de eixos cartesianos ortogonais, as representações gráficas das funções reais f(x) = x² – 2x – 3 e g(x) = – x² + 4x – 5 são parábolas. A distância entre os seus vértices é igual a:
a) 3√2
b) √26
c) √10
d) 2√3
e) 2√10
16. (PUC-RJ) - Sabendo que o ponto B = (3,b) é equidistante dos pontos A = (6,0) e C = (0,6), então b vale:
a) 1
b) 2
c) 3
d) 4
e) 5
17. (PUC-RJ) - Se os pontos A = (-1, 0), B = (1, 0) e C = (x, y) são vértices de um triângulo equilátero, então a distância entre A e C é:
a) 1
b) 2
c) 4
d) √2
e) √3
18. (UFMG) - Seja Q (-1, a) um ponto do 3º quadrante.O valor de a, para que a distância do ponto P (a, 1) ao ponto Q seja igual a 2, é:
a) - 1 - √2
b) 1 - √2
c) 1 + √2
d) -1 + √2
e) - 1
19. (ITA - SP) - Três pontos de coordenadas,respectivamente, (0, 0), (b, 2b) e (5b, 0), com b > 0, são vértices de um retângulo. As coordenadas do quarto vértice são dadas por:
a) (- b, - b)
b) (2b, - b)
c) (4b, - 2b)
d) (3b, - 2b)
e) (2b, - 2b)
20. (PUC - SP) - Dados A(4, 5), B(1, 1) e C(x, 4), o valor de x para que o triângulo ABC seja retângulo em B é:
a) 3
b) 2
c) 0
d) - 3
e) - 2
01
|
02
|
03
|
04
|
05
|
06
|
07
|
08
|
09
|
10
|
| A | B | C | A | A | C | A | E | D | |
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
| C | B | B | E | C | C | B | E | C | D |