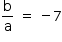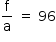Um polinômio de quinto grau tem 2 como uma raiz de multiplicidade 3. A razão entre o coeficiente do termo de quarto grau e o coeficiente do termo de quinto grau é igual a –7. A razão entre o termo independente e o coeficiente do termo de quinto grau é igual a 96. A menor raiz desse polinômio vale
a) 0
b) –1
c) –2
d) –3
-------------------------------------------------------------------- RESPOSTA: D
👀 Resposta comentada 👇
Como o polinômio é do 5º grau, sua lei P(x) pode ser escrita como P(x) = ax5 + bx4 + cx3 + dx2 + ex + f, em que a, b, c, d, e e f são constantes, com a ≠ 0.
Do enunciado, tem-se:
Sejam x1, x2, x3, x4 e x5 as raízes da equação P(x) = 0, com x1 = x2 = x3 = 2.
Pelas relações de Girard, tem-se:
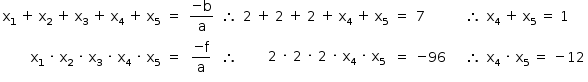
Resolvendo-se o sistema de equações
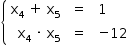
tem-se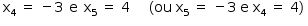 
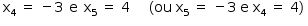
Logo, a menor raiz é –3.
(https://angloresolve.plurall.net/#topo)