Na figura estão representadas três retas no plano
cartesiano, sendo P, Q e R os pontos de intersecções entre
as retas, e A, B e C s pontos de intersecções dessas retas
com o eixo x.
Essa figura é a representação gráfica de um sistema linear
de três equações e duas incógnitas que
a) possui três soluções reais e distintas, representadas
pelos pontos P, Q e R, pois eles indicam onde as retas
se intersectam.
b) possui três soluções reais e distintas, representadas
pelos pontos A, B e C, pois eles indicam onde as retas
intersectam o eixo das abscissas.
c) possui infinitas soluções reais, pois as retas se
intersectam em mais de um ponto.
d) não possui solução real, pois não há ponto que pertença
simultaneamente às três retas.
e) possui uma única solução real, pois as retas possuem
pontos em que se intersectam.
Cada uma dessas três retas pode ser representada por uma equação linear de coeficientes reais, nas incógnitas x e y:
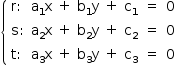
Uma solução desse sistema consiste em um par (x, y) que satisfaça simultaneamente as 3 equações.
Graficamente, o sistema terá solução se existir um ponto (x, y) que pertence às três retas ao mesmo tempo, o que não ocorre na figura dada no enunciado.
Logo, o sistema não possui solução real, pois não há um ponto que pertença simultaneamente às três retas

