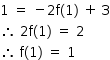Seja f(x) uma função tal que para todo número real x temos que xf(x − 1) = (x − 3)f(x) + 3. Então, f(1) é igual a
a) 0.
b) 1.
c) 2.
d) 3.
👀 Resposta comentada:
Fazendo-se x = 1, tem-se:
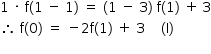
Fazendo-se x = 0, tem-se:
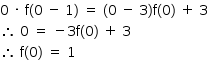
Substituindo-se f(0) = 1 em (I), tem-se: