(UNICAMP-2017) - QUESTÃO

Considere as funções f(x) = 3x e g(x) = x³ , definidas para todo número real x. O número de soluções da equação f(g(x)) = g(f(x)) é igual a

a) 1. 

b) 2. 

c) 3.

d) 4.

-------------------------------------------------------------------- RESPOSTA: C

👀 Resposta comentada:

Considerando-se as funções f(x) = 3x e g(x) = x3, tem-se:

De f(g(x)) = g(f(x)), tem-se:

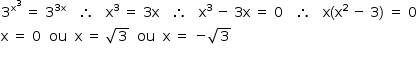
Logo, o número de soluções da equação é 3.