Sejam a e b números reais. Considere, então, os dois sistemas lineares abaixo, nas variáveis x, y e z:
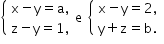
Sabendo que esses dois sistemas possuem uma solução em comum, podemos afirmar corretamente que
a) a - b = 0.
b) a + b = 1.
c) a - b = 2.
d) a + b = 3.
👀 Resposta comentada:
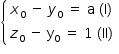
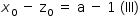
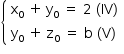
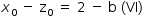
Logo, a + b = 3
Sendo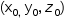 
a solução comum dos dois sistemas, do primeiro sistema tem-se:
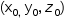a solução comum dos dois sistemas, do primeiro sistema tem-se: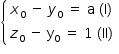
Ao fazer-se a subtração membro a membro de (I) e (II), tem-se:
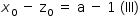
Do segundo sistema, tem-se:
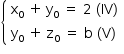
Ao fazer-se a subtração membro a membro de (IV) e (V), tem-se:
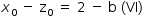
De (III) e (VI), tem-se que a – 1 = 2 – b.
Logo, a + b = 3