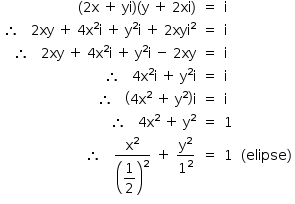Seja i a unidade imaginária, isto é, i² = −1. O lugar geométrico dos pontos do plano cartesiano com coordenadas reais (x, y) tais que (2x + yi)(y + 2xi) = i é uma
a) elipse.
b) hipérbole.
c) parábola.
d) reta.
-------------------------------------------------------------------- RESPOSTA: A
👀 Resposta comentada:
Do enunciado, tem-se que: