(Albert Einstein 2017) - QUESTÃO

Uma matriz B possui i linhas e j colunas e seus elementos são obtidos a partir da expressão bij = i – 2j. Seja uma matriz A= (aij)2x3 cujos elementos da primeira coluna são nulos e I2 a matriz identidade de ordem 2, tal 2 que AB = I2 . O valor numérico do maior elemento da 2 matriz A é igual a

a) 0

b) 1

c) 2

d) 3

-------------------------------------------------------------------- RESPOSTA: B

👀 Resposta comentada 👇

Se A é do tipo 2 x 3 e B é do tipo i x j, para que a multiplicação AB exista, é necessário que i = 3; além disso, para que AB = I2, deve-se ter j = 2. Assim, conclui-se que B é do tipo 3 x 2 e, dado que bij = i - 2j, tem-se a matriz

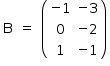
Sabe-se, do enunciado, que a matriz A é da forma:

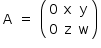
De AB = I2, tem-se a seguinte equação matricial:

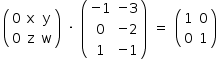
Reescrevendo-se na forma de sistema, tem-se:

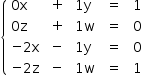
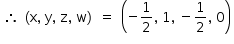
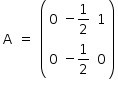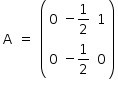Logo, , de modo que o valor numérico do maior elemento é 1.