Um lapidador recebeu de um joalheiro a encomenda para
trabalhar em uma pedra preciosa cujo formato é o de uma
pirâmide, conforme ilustra a Figura 1. Para tanto, o
lapidador fará quatro cortes de formatos iguais nos cantos
da base. Os cantos retirados correspondem a pequenas
pirâmides, nos vértices P, Q. R e S, ao longo dos segmentos tracejados, ilustrados na Figura 2.
Depois de efetuados os cortes, o lapidador obteve, a partir
da pedra maior, uma joia poliédrica cujos números de
faces, arestas e vértices são, respectivamente, iguais a
a) 9, 20 e 13.
b) 9, 24 e 13.
c) 7, 15 e 12.
d) 10, 16 e 5.
e) 11, 16 e 5.
Da figura do enunciado, temos:
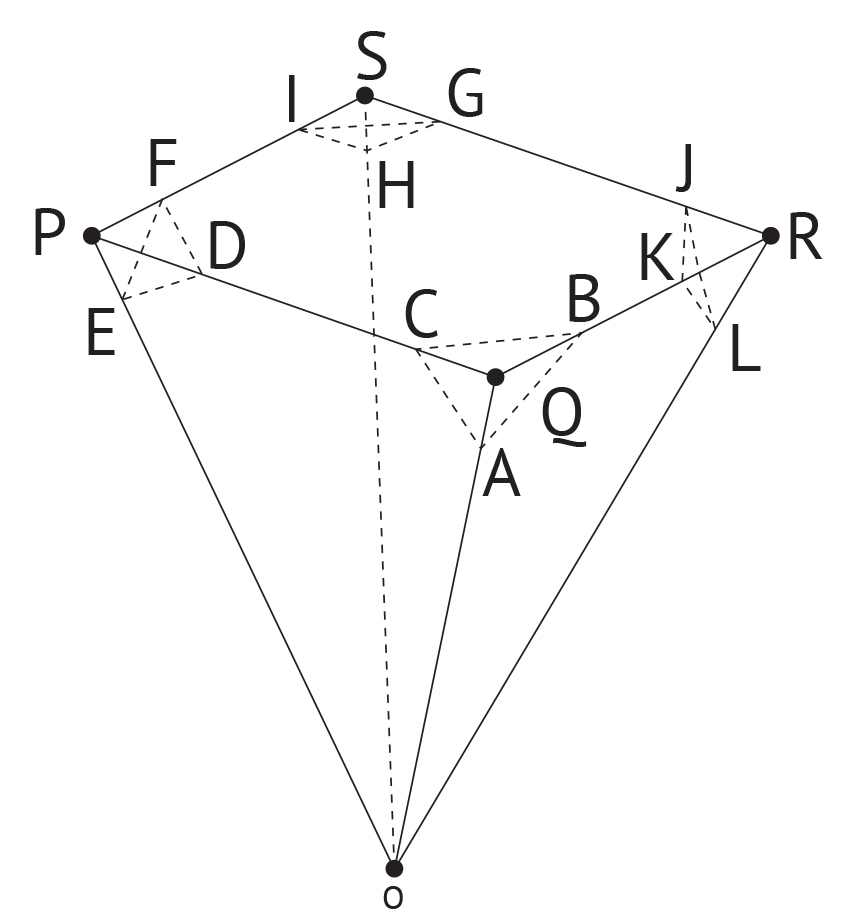
- Após os cortes, o lapidador obteve um sólido formado por quatro pentágonos (OACDE, OABKL, OHGJL e OHIFE), quatro triângulos (ABC, DEF, GHI e JKL) e um octógono (BCDFIGJK); assim, o total de faces desse sólido é 9;
- Os vértices desse sólido são os pontos A, B, C, D, E, F, G, H, I, J, K, L e O e, portanto, o sólido possui um total de 13 vértices;
- Cada face pentagonal possui 5 arestas; cada face triangular possui 3 arestas e a face octogonal possui 8 arestas. Desta forma, teríamos um total de 4 · 5 + 4 · 3 + 1 · 8 = 40 arestas; no entanto, cada aresta é comum a duas faces, de modo que o total de arestas será
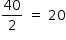 .
. - Assim, o sólido terá 9 faces, 20 arestas e 13 vértices.

